| Вид числового множества | Определение множества | Какие операции выполнимы в этом множестве | Примечания |
|---|---|---|---|
| Множество натуральных чисел \(\mathbb N\). | Числа \(1,2,3,4,5,\dots\), т.е. числа, используемые при счёте предметов. | Множество \(\mathbb N\) замкнуто относительно прямых операций: сложение, умножение, возведение в степень. | В множестве натуральных чисел вводят понятия простого и составного числа, НОД, НОК. В русскоязычной литературе, в русской математической школе, принято не считать \(0\) натуральным числом. Все натуральные числа образуют ряд натуральных чисел. |
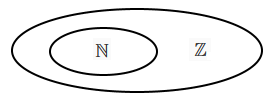
| Множество целых чисел \(\mathbb Z\). | К множеству \(\mathbb N\) присоединим число 0 и целые отрицательные числа. | Множество \(\mathbb Z\) замкнуто относительно операций сложения, умножения, возведения в степень, вычитания. | Множество целых чисел включает в себя множество натуральных чисел: \(\mathbb N \subset \mathbb Z\).
|
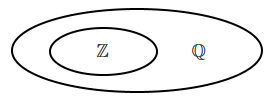
| Множество рациональных чисел \(\mathbb Q\). | Рациональным числом называется число, представимое в виде \(\dfrac{a}{b}\) (обыкновенной дроби), где \(a\) - это числитель, \(b\) - это знаменатель. | Множество рациональных чисел \(\mathbb Q\) замкнуто относительно операций сложения, умножения, возведения в степень, вычитания, деления. | Дробь вида \(\dfrac{a}{b}\), где \(b=10^n, n\in\mathbb N\), называется десятичной. Всякое рациональное число представимо в виде конечной или бесконечной периодической десятичной дроби. Множество рациональных чисел включает в себя множество целых чисел.
|
| Множество иррациональных чисел \(\mathbb I\). | Иррациональное число - это число, не представимое в виде обыкновенной дроби. | Множество иррациональных чисел не замкнуто относительно ни одной операции. | Иррациональные числа представимы в виде бесконечной непериодической десятичной дроби. |
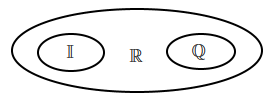
| Множество действительных чисел \(\mathbb R\). | Множество действительных чисел - это объединение множества рациональных чисел и множества иррациональных чисел. | Множество действительных чисел \(\mathbb R\) замкнуто относительно всех алгебраических операций, кроме извлечения корня. Не существует корня четной степени из отрицательного числа. | Всякое действительное число - десятичная дробь (периодическая или непериодическая бесконечная).
|
Комментарий. Выражение "множество замкнуто относительно операции" означает, что совершая данную операцию с членом этого множества, вы снова получаете член того же множества. Например, перемножая два натуральных числа, вы всегда получите натуральное число. А вот вычисляя разность двух натуральных чисел, вы далеко не всегда "останетесь" во множестве натуральных чисел - например, \(10 - 12 = -2\), а число \(-2\) не натуральное!
Простое число - это число, которое делится только на 1 и самого себя. Простых чисел бесконечно много. Единственное четное простое число - 2. Пример простых чисел: 2, 3, 7, 23, 47...
Взаимно обратные числа - это числа, произведение которых равно 1.
Взаимно простые числа - это числа, у которых единственный общий делитель - 1.
НОД - наибольший общий делитель(наибольшее число на которое одновременно делятся два или более чисел)
НОК- наименьшее общее кратное(наименьшее число, которое делится одновременно на два или более различных чисел