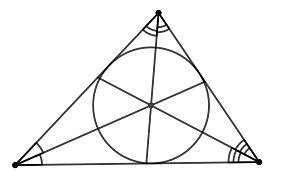
Любой треугольник можно описать около окружности.
Центр окружности, вписанной в треугольник, лежит на пересечении биссектрис.
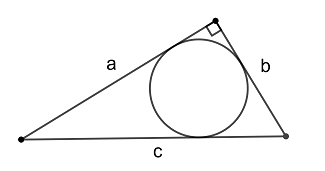
Радиус окружности, вписанной в прямоугольный треугольник, равен \(\dfrac{a+b-c}{2}\), где \(a\) и \(b\) - это катеты, \(c\) - гипотенуза.
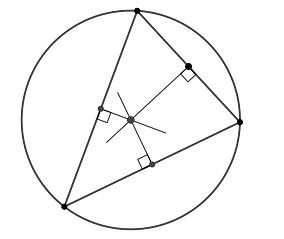
Около любого треугольника можно описать окружность.
Центр окружности, описанной около треугольника, лежит на пересечении срединных перпендикуляров.
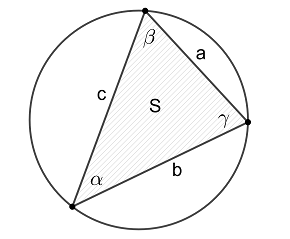
Радиус окружности, описанной около треугольника, равен:
- произведению длин всех сторон, поделённому на 4 площади треугольника: \(\dfrac{abc}{4S}\);
- отношению длины стороны треугольника к удвоенному синусу противолежащего этой стороне угла: \(\dfrac{a}{2\sin\alpha} = \dfrac{b}{2\sin\beta} = \dfrac{c}{2\sin\gamma}\).
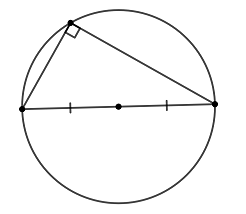
Радиус окружности, описанной около прямоугольного треугольника, равен половине гипотенузы.
Теорема синусов.
Стороны треугольника пропорциональны синусам противолежащих углов.
\(\dfrac{a}{\sin\alpha} = \dfrac{b}{\sin\beta} = \dfrac{c}{\sin\gamma}\).