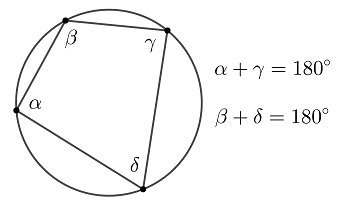
Выпуклый четырехугольник вписан в окружность тогда и только тогда, когда сумма противолежащих углов равна \(180^\circ\)
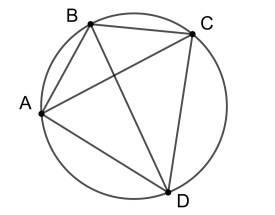
Теорема Птолемея.
Произведение длин диагоналей четырехугольника, вписанного в окружность, равно сумме произведений длин противоположных сторон.
(\(AC \cdot BD = AB \cdot CD + BC \cdot AD\))
Признак вписанного четырехугольника.
Если произведения отрезков диагоналей выпуклого четырехугольника равны, то данный четырехугольник вписан в окружность.

Выпуклый четырехугольник описан около окружности тогда и только тогда, когда суммы противолежащих сторон равны.