Параллельные прямые
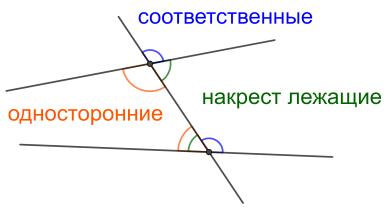
При пересечении двух прямых \(a\) и \(b\) третьей прямой - \(c\) (секущей) образуются углы:
● Накрест лежащие
● Соответственные
● Односторонние
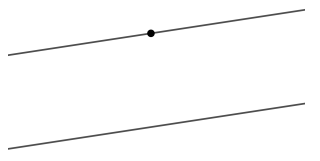
Прямые называются параллельными, если они не пересекаются.
Аксиома параллельных прямых: Через точку, не лежащую на данной прямой, можно провести прямую, параллельную данной, и при этом только одну.
Признаки параллельности прямых.
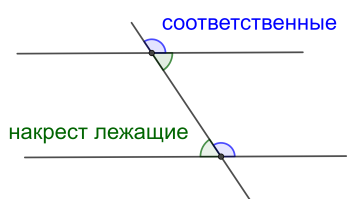
● Если при пересечении двух прямых третьей, накрест лежащие углы равны, то прямые параллельны.
● Если при пересечении двух прямых третьей, соответственные углы равны, то прямые параллельны.
● Если при пересечении двух прямых третьей, односторонние углы образуют в сумме \(180^{\circ}\), то прямые параллельны.
Свойства параллельных прямых
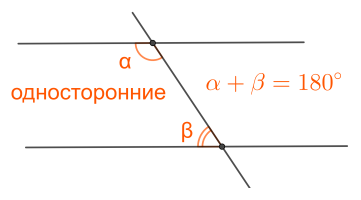
Если две параллельные прямые \(a\) и \(b\), пересечены третьей - \(c\) (секущей), то получившиеся...
● Накрест лежащие углы равны.
● Соответственные углы равны.
● Односторонние углы образуют в сумме \(180^{\circ}\).