Теоремы
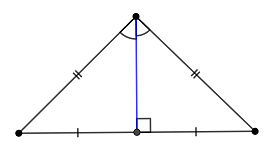
Теорема (Свойство медианы равнобедренного треугольника)
Медиана равнобедренного треугольника, опущенная на основание, является и высотой, и биссектрисой.
Теорема (Признаки равнобедренного треугольника)
Если в треугольнике медиана, проведенная к одной из сторон, является высотой, то данный треугольник равнобедренный.
Если в треугольнике медиана, проведенная к одной из сторон, является биссектрисой, то данный треугольник равнобедренный.
Теорема (Свойство биссектрисы равнобедренного треугольника)
Биссектриса равнобедренного треугольника, опущенная на основание, является и высотой и медианой.
Теорема (Признаки равнобедренного треугольника)
Если в треугольнике биссектриса является медианой, то данный треугольник равнобедренный.
Если в треугольнике биссектриса является высотой, то данный треугольник равнобедренный.
Теорема (Свойство высот равнобедренного треугольника)
В равнобедренном треугольнике высота является и медианой и биссектрисой.
Теорема (Признаки равнобедренного треугольника)
Если в треугольнике высота является медианой, то данным треугольник равнобедренный.
Если в треугольнике высота является биссектрисой, то данным треугольник равнобедренный.
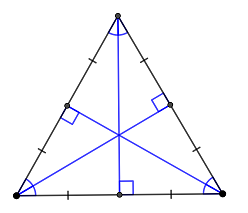
Теорема (Свойства высот, медиан и биссектрис)
В равностороннем треугольнике любая биссектриса является и высотой, и медианой.
В равностороннем треугольнике любая высота является и биссектрисой, и медианой.
В равностороннем треугольнике любая медиана является и высотой, и биссектрисой.
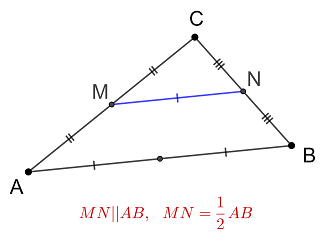
Средняя линия треугольника - отрезок, соединяющий середины двух сторон треугольника.
Теорема (Свойства средней линии)
Средняя линия параллельна стороне, которую она не пересекает, и равна ее половине.
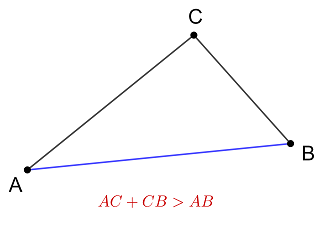
Теорема (Неравенство треугольника)
Сумма двух любых сторон треугольника всегда больше третьей стороны.