Эволюция понятия числа.

Когда-то была объявлена премия за написание книги на тему "Как человек без числа жил". Она осталась так и не выданной - оказалось, что невозможно изобразить/вообразить жизнь даже первобытного человека без понятия числа.

Конечно, в самом начале люди не пользовались привычным нам понятием числа, а тем более привычными нам цифрами для написания чисел. Они пользовались пальцами, камнями, засечками на деревьях, рисунками и т.п. Так как число, само по себе, необязательно для установления количественного соотношения между группами объектов, то люди долгое время пользовались просто умением сравнивать совокупности, никак не называя количество предметов в совокупности. Подумайте, как можно, не называя чисел, сравнить 10 баранов и 8 баранов?

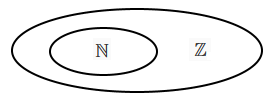
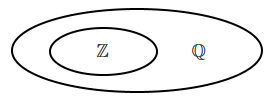
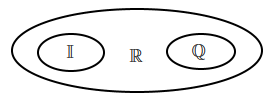
Таким образом, в математике сначала было не число, а множество. И очевидно, что для подсчёта объектов в множестве использовали то, что мы сейчас называем натуральными числами (целыми , положительными). Потом к этим элементарным вычислениям добавились вычисления с помощью отношений чисел - то, что мы сейчас называем обыкновенными дробями. Дальше выяснилось, что для некоторых целей геометрии и астрономии имеющихся чисел недостаточно - например, отношение длины диагонали квадрата к длине его стороны не может быть представлено ни натуральным, ни рациональным (дробь) числом. Появляются иррациональные числа. Существует даже такая легенда: Пифагор почитал числа как нечто божественное, он видел в них гармонию и красоту, учил, что все числа могут быть выражены как отношения целых чисел. И когда один из его учеников, Гиппас, заговорил о числе, которое не укладывалось в существующие понятия - диагональ квадрата со стороной 1, этого ученика казнили.

С течением времени потребность в вычислениях росла, множества, которые необходимо было сравнивать, увеличивались, появилась необходимость в записях. Появились цифры. Привычные нам цифры, в том числе очень важная цифра "0", мы привыкли называть арабскими, хотя на самом деле придуманы они были в Индии. Возникла десятичная, позиционная система счисления. Есть разные версии, объясняющие почему человек выбрал десятичную систему. Самая распространенная и очевидная - потому, что у людей 10 пальцев на руках.

Итак, есть 10 цифр - 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Количественная характеристика числа зависит от позиции цифры в этом числе. Например, числа 101 и 110 состоят из одних и тех же цифр, но числа эти конечно же не равны друг другу.

В нашей жизни встречаются и другие системы счисления. Например, время мы измеряем в шестидесятеричной системе счисления, а компьютеры, смартфоны, планшеты и прочая электроника используют двоичную систему счисления.

Конечно, на иррациональных числах развитие понятия числа не закончилось. Но мы пока остановимся на них и дальше иррациональных чисел не пойдём.

Вид числового множества	Определение множества	Какие операции выполнимы в этом множестве	Примечания
Множество натуральных чисел \(\mathbb N\).	Числа \(1,2,3,4,5,\dots\), т.е. числа, используемые при счёте предметов.	Множество \(\mathbb N\) замкнуто относительно прямых операций: сложение, умножение, возведение в степень.	В множестве натуральных чисел вводят понятия простого и составного числа, НОД, НОК. В русскоязычной литературе, в русской математической школе, принято не считать \(0\) натуральным числом. Все натуральные числа образуют ряд натуральных чисел.
Множество целых чисел \(\mathbb Z\).	К множеству \(\mathbb N\) присоединим число 0 и целые отрицательные числа.	Множество \(\mathbb Z\) замкнуто относительно операций сложения, умножения, возведения в степень, вычитания.	Множество целых чисел включает в себя множество натуральных чисел: \(\mathbb N \subset \mathbb Z\).
Множество рациональных чисел \(\mathbb Q\).	Рациональным числом называется число, представимое в виде \(\dfrac{a}{b}\) (обыкновенной дроби), где \(a\) - это числитель, \(b\) - это знаменатель.	Множество рациональных чисел \(\mathbb Q\) замкнуто относительно операций сложения, умножения, возведения в степень, вычитания, деления.	Дробь вида \(\dfrac{a}{b}\), где \(b=10^n, n\in\mathbb N\), называется десятичной. Всякое рациональное число представимо в виде конечной или бесконечной периодической десятичной дроби. Множество рациональных чисел включает в себя множество целых чисел.
Множество иррациональных чисел \(\mathbb I\).	Иррациональное число - это число, не представимое в виде обыкновенной дроби.	Множество иррациональных чисел не замкнуто относительно ни одной операции.	Иррациональные числа представимы в виде бесконечной непериодической десятичной дроби.
Множество действительных чисел \(\mathbb R\).	Множество действительных чисел - это объединение множества рациональных чисел и множества иррациональных чисел.	Множество действительных чисел \(\mathbb R\) замкнуто относительно всех алгебраических операций, кроме извлечения корня. Не существует корня четной степени из отрицательного числа.	Всякое действительное число - десятичная дробь (периодическая или непериодическая бесконечная).

Комментарий. Выражение "множество замкнуто относительно операции" означает, что совершая данную операцию с членом этого множества, вы снова получаете член того же множества. Например, перемножая два натуральных числа, вы всегда получите натуральное число. А вот вычисляя разность двух натуральных чисел, вы далеко не всегда "останетесь" во множестве натуральных чисел - например, \(10 - 12 = -2\), а число \(-2\) не натуральное!

Простое число - это число, которое делится только на 1 и самого себя. Простых чисел бесконечно много. Единственное четное простое число - 2. Пример простых чисел: 2, 3, 7, 23, 47...

Взаимно обратные числа - это числа, произведение которых равно 1.

Взаимно простые числа - это числа, у которых единственный общий делитель - 1.

НОД - наибольший общий делитель(наибольшее число на которое одновременно делятся два или более чисел)

НОК- наименьшее общее кратное(наименьшее число, которое делится одновременно на два или более различных чисел

Арифметические действия можно условно поделить на "прямые" и "обратные".
Прямые - сложение, умножение, возведение в степень.
Обратные действия - вычитание, деление, извлечение корня, определяются через прямые.

Вычесть из числа \(A\) число \(B\) - это значит найти такое число \(C\), которое при сложении с \(B\) даст \(A\): \(A - B = C\) означает, что \(A = C + B\).
Компоненты вычитания:
A - уменьшаемое
B - вычитаемое
C - разность

Если в задаче сказано, что разность \(a\) и \(b\) равна \(c\), или что первая машина приехала на час раньше второй, или что Вася съел на три конфеты больше, чем Петя, или что один угол больше другого на 30 градусов, то все эти утверждения в переводе на математический язык, в виде равенств, можно записать именно как разность (\(A - B = C\)).

Разделить число \(A\) на число \(B\) нацело - это значит найти такое число \(C\), что \(A\), умноженное на \(B\), равно \(C\): \(A : B = C\) означает, что \(A = C \cdot B\).
Компоненты деления:
A - делимое
B - делитель
C - частное

Таким образом, если про некоторое число \(p\) известно, что оно делится нацело, например, на 17, то это означает, что данное число можно записать в виде \(p=17k\), где \(k\) - натуральное число. Говорят, что \(p\) представлено в виде произведения \(17\) и \(k\).

Извлечь корень степени \(n\) из числа \(A\) - это значит найти такое число \(C\), что \(C\), возведенное в степень \(n\), будет равно \(A\): \(A = C^n\).

Иногда используется понятие арифметический квадратный корень. Арифметическим квадратным корнем из числа \(A\) называется неотрицательное число, квадрат которого равен данному числу \(A\).