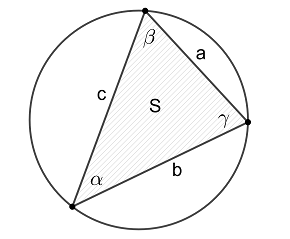
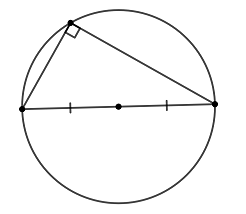
Отрезки в окружности
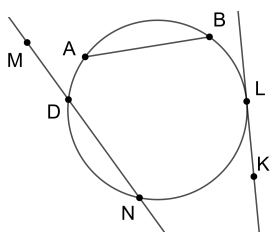
Касательная - прямая, имеющая одну общую точку с окружностью.
Секущая - прямая, имеющая две общие точки с окружностью.
Хорда - отрезок, соединяющий две любые точки окружности.
Свойства касательной
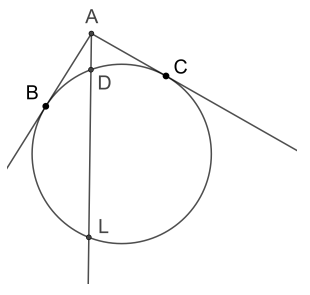
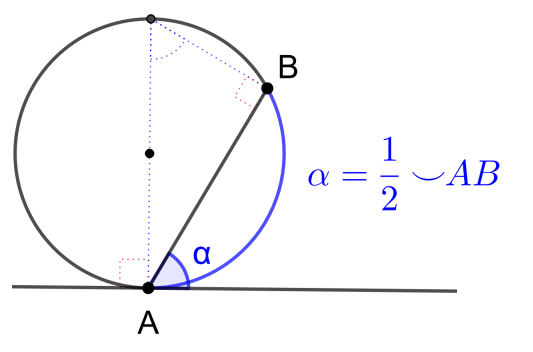
● Радиус окружности перпендикулярен касательной в точке касания.
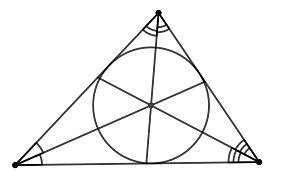
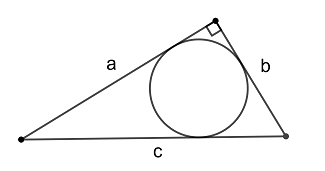
● Отрезки касательных, проведенных из одной точки к окружности, равны.
● Квадрат касательной равен произведению секущей на ее внешнюю часть.
(\(AB = AC\), \(AB^2 = AD\cdot AL\))
Свойства хорд
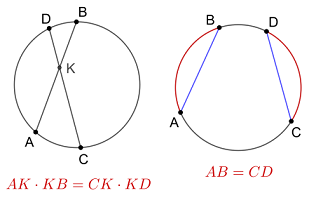
● Произведения отрезков пересекающихся хорд равны.
● Равные хорды отсекают равные дуги.
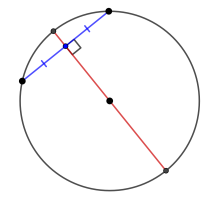
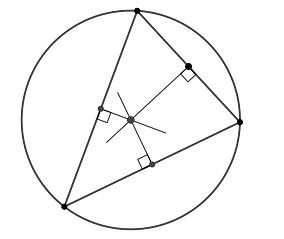
● Диаметр окружности перпендикулярный хорде делит ее пополам.
● Если диаметр делит хорду пополам, то он перпендикулярен данной хорде.
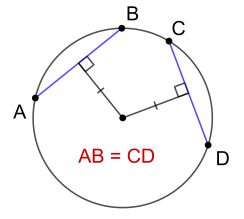
● Хорды, равноудаленные от центра, равны.
● Если хорды равны, то они равноудалены от центра.
Задача. Доказать, что если 2 секущие проведены из одной точки, то произведение одной секущей на ее внешнюю часть равно произведению другой секущей на ее внешнюю часть. Если диаметр перпендикулярен хорде, то он проходит через ее середину