Геометрия. Углы.

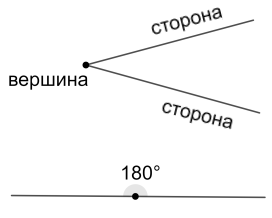
Угол - это фигура, образованная двумя лучами - сторонами угла, исходящими из общей точки - вершины угла.

Развернутый угол – это угол, стороны которого являются дополнительными полупрямыми. Градусная мера развернутого угла - \(180^{\circ}\).

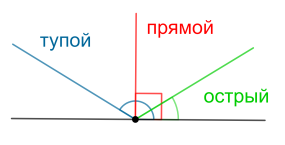
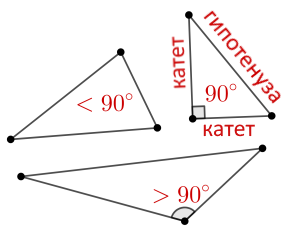
Тупой угол – угол больше \(90^{\circ}\) градусов, но меньше \(180^{\circ}\).

Острый угол – угол больше \(0^{\circ}\), но меньше \(90^{\circ}\).

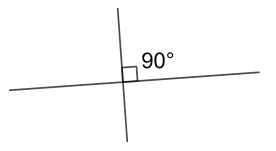
Прямой угол – угол равный \(90^{\circ}\).

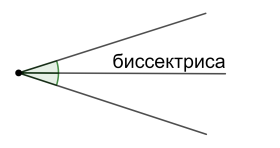
Биссектриса угла – луч, который исходит из вершины угла, проходит между сторонами угла и делит угол на два равных.

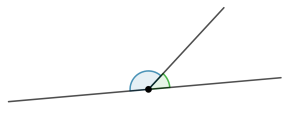
Смежные углы – это углы, у которых одна сторона общая, а две другие дополняют друг друга до прямой.

Свойство смежных углов: Сумма смежных углов равна \(180^{\circ}\).

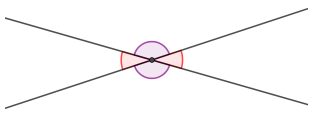
Вертикальные углы – два угла называются вертикальными, если стороны одного являются продолжением сторон другого.

Свойство вертикальных углов: Вертикальные углы равны.

Перпендикулярные прямые – это прямые, пересекающиеся под прямым углом. То есть, две прямые, образующие при пересечении угол в \(90^{\circ}\).

Перпендикуляром называется отрезок прямой, перпендикулярной данной, который одним из своих концов имеет точку пересечения прямых.

Эта точка называется основанием перпендикуляра.

А длина отрезка называется расстоянием от точки до прямой.

Кратчайшее расстояние от точки до прямой - перпендикуляр от данной точки к прямой.

При пересечении двух прямых \(a\) и \(b\) третьей прямой - \(c\) (секущей) образуются углы:

● Накрест лежащие
● Соответственные
● Односторонние

Прямые называются параллельными, если они не пересекаются.

Аксиома параллельных прямых: Через точку, не лежащую на данной прямой, можно провести прямую, параллельную данной, и при этом только одну.

● Если при пересечении двух прямых третьей, накрест лежащие углы равны, то прямые параллельны.
● Если при пересечении двух прямых третьей, соответственные углы равны, то прямые параллельны.
● Если при пересечении двух прямых третьей, односторонние углы образуют в сумме \(180^{\circ}\), то прямые параллельны.

Если две параллельные прямые \(a\) и \(b\), пересечены третьей - \(c\) (секущей), то получившиеся...
● Накрест лежащие углы равны.
● Соответственные углы равны.
● Односторонние углы образуют в сумме \(180^{\circ}\).

Сумма углов любого треугольника равна \(180^\circ\).

Внешний угол треугольника - это угол, смежный с одним из его внутренних углов.

Внешний угол треугольника равен сумме двух внутренних, не смежных с ним.

● Если в треугольники все углы острые, то такой треугольник остроугольный.
● Если в треугольнике один угол тупой, то такой треугольник тупоугольный.
● Если в треугольнике один угол прямой, то такой треугольник прямоугольный.

Стороны прямоугольного треугольника: катет, катет, гипотенуза.
Гипотенуза лежит напротив прямого угла.

Фигуры называются равными, если их можно совместить наложением.

● По стороне и двум прилежащим углам.
Два треугольника равны, если сторона и два прилежащих к ней угла одного треугольника равны стороне и двум прилежащим к ней углам другого треугольника.

● По двум сторонам и углу между ними.
Если две стороны и угол между ними одного треугольника равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

● По трем сторонам.
Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.

Из равенства треугольников следует равенство всех их элементов.
В равных треугольниках напротив равных сторон лежат равные углы и наоборот.

Равнобедренный треугольник - треугольник, у которого две стороны равны. Эти стороны называются боковыми, а третья сторона – основанием.

Свойство равнобедренного треугольника: У равнобедренного треугольника углы при основании равны.

Признак равнобедренного треугольника: Если у треугольника два угла равны, то такой треугольник - равнобедренный.

Равносторонний треугольник – это треугольник, у которого все стороны равны.

Свойство равностороннего треугольника: У равностороннего треугольника все углы равны.

Признак равностороннего треугольника: Если у треугольника все углы равны, то данный треугольник равносторонний.

Срединный перпендикуляр к отрезку - это прямая проведенная к середине отрезка и перпендикулярная ему.

Высота треугольника - это перпендикуляр, опущенный из вершины треугольника к противоположной стороне или ее продолжению.

Высоты треугольника пересекаются в одной точке.

Биссектриса угла треугольника - это отрезок биссектрисы угла, заключенный между вершиной треугольника и противоположной стороной.

Биссектрисы треугольника пересекаются в одной точке.

Свойство биссектрисы угла: Любая точка биссектрисы равноудалена от сторон угла.

Признак биссектрисы: точка равноудаленная от сторон угла, лежит на биссектрисе данного угла.

Медиана треугольника - соединяет вершину треугольника и середину противоположной стороны.

Медианы треугольника пересекаются в одной точке.

Срединный перпендикуляр треугольника - это срединный перпендикуляр проведенный к стороне треугольника.

Свойство: Любая точка срединного перпендикуляра равноудалена от концов отрезка.

Признак: Точка равноудаленная от концов отрезка лежит на срединном перпендикуляре.

Теорема (Свойство медианы равнобедренного треугольника)
Медиана равнобедренного треугольника, опущенная на основание, является и высотой, и биссектрисой.

Теорема (Признаки равнобедренного треугольника)
Если в треугольнике медиана, проведенная к одной из сторон, является высотой, то данный треугольник равнобедренный.
Если в треугольнике медиана, проведенная к одной из сторон, является биссектрисой, то данный треугольник равнобедренный.

Теорема (Свойство биссектрисы равнобедренного треугольника)
Биссектриса равнобедренного треугольника, опущенная на основание, является и высотой и медианой.

Теорема (Признаки равнобедренного треугольника)
Если в треугольнике биссектриса является медианой, то данный треугольник равнобедренный.
Если в треугольнике биссектриса является высотой, то данный треугольник равнобедренный.

Теорема (Свойство высот равнобедренного треугольника)
В равнобедренном треугольнике высота является и медианой и биссектрисой.

Теорема (Признаки равнобедренного треугольника)
Если в треугольнике высота является медианой, то данным треугольник равнобедренный.
Если в треугольнике высота является биссектрисой, то данным треугольник равнобедренный.

Теорема (Свойства высот, медиан и биссектрис)
В равностороннем треугольнике любая биссектриса является и высотой, и медианой.
В равностороннем треугольнике любая высота является и биссектрисой, и медианой.
В равностороннем треугольнике любая медиана является и высотой, и биссектрисой.

Средняя линия треугольника - отрезок, соединяющий середины двух сторон треугольника.

Теорема (Свойства средней линии)
Средняя линия параллельна стороне, которую она не пересекает, и равна ее половине.

Теорема (Неравенство треугольника)
Сумма двух любых сторон треугольника всегда больше третьей стороны.

Треугольник, у которого один угол прямой, называется прямоугольным.
Стороны, пересекающиеся под прямым углом, называются катетами.
Сторона, лежащая напротив прямого угла, называется гипотенузой.
Гипотенуза всегда длиннее любого из катетов.

Теорема (Признаки равенства прямоугольных треугольников)
Если катеты одного прямоугольного треугольника равны катетам другого прямоугольного треугольника, то такие треугольники равны.
Если катет и гипотенуза одного прямоугольного треугольника равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны.
Если катет и острый угол одного прямоугольного треугольника равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.
Если гипотенуза и острый угол одного прямоугольного треугольника равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.

Сумма острых углов прямоугольного треугольника равна \(90^\circ\).
Медиана прямоугольного треугольника, опущенная на гипотенузу, равна половине гипотенузы.

Катет, лежащий напротив угла в \(30^\circ\), равен половине гипотенузы.